+
+
 =
=

Howard Zhou & Jie Sun
Seamless Cloning
seamless insertion with rectangular boundary condition
 +
+
 =
=

inserting objects with holes
 +
+
 =
=

inserting transparent objects
 +
+
 =
=

Selection Editing
Local illumination change



alpha = 0.05, beta = 0.2 alpha = 0.05, beta = 0.4
texture flattening
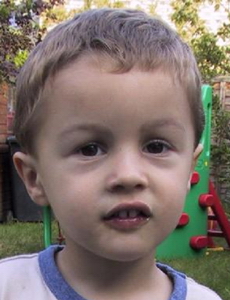
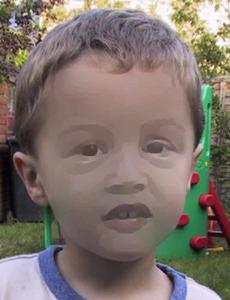
edge detection image


The result is achieved using the first edge detection image (the scary one). The second edge detection has higher edge threshold and gives a much worse texture flattening result. This tells us that the edge detection stage is essential for texture flattening to work well.
seamless tiling




Some more examples since we have those texture lying around















The following example shows that the result would not be good when the seam really doesn't fit




Motivation
Our approach
Texture Flattening + Image Analogy
Using Image Analogy idea (specifically, texture by number)
Reference: A. Hertzmann, et.al. "Image Analogy", SIGGRAPH 2001

|
: |

|
:: |

|
: |

|
A |
A' |
B |
B' |
The images on the left are training data; our system "learns" the transformation from A to A', and then applies that transformation to B to get B'. In other words, we compute B' to complete the analogy.
One of the application of Image Analogy is: Texture by number, which is also used to generate some terrain like image.
 |
: |
 |
:: |
Unfiltered source (A) |
Filtered source (A') |
||
 |
: |
 |
|
Unfiltered target (B) |
Filtered target (B') |
Here, the problem is how to generate unfiltered source (A). In texture by number those segmentation is manually generated. We want to have an automatic way of generating (A)
Our method uses
Our result


edge detection texture flattening


after blurring (A) (A')


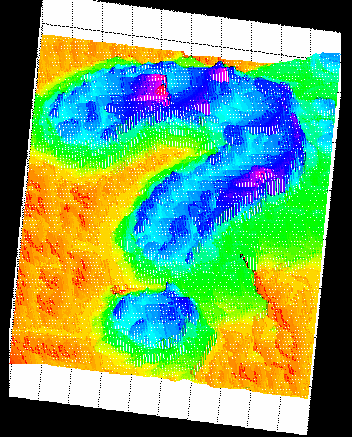
(B) (B')
Texture synthesis on Laplacian + piecewise seamless tiling
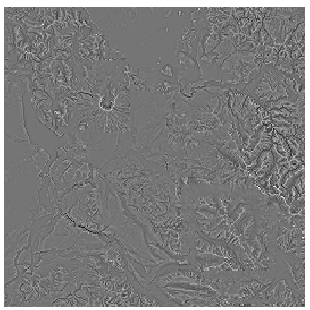
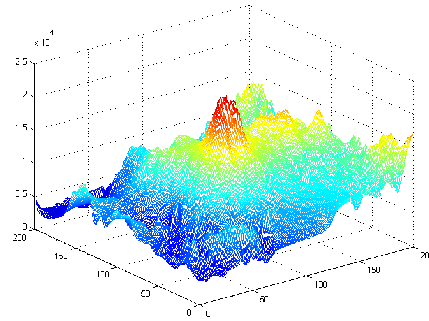
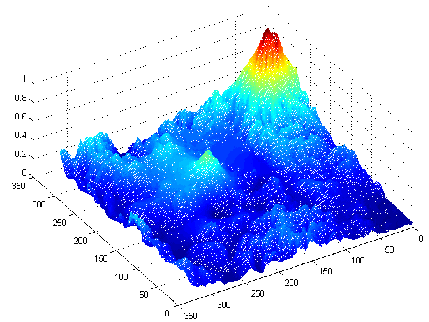
(A)Example of synthesized laplacian (B)Solution of the poisson equation (C)Result comparison
Current Algorithm:
1. Regard the laplacian image as a regular image
2. Do texture synthesis with laplacian images (image quilting/graph cut/...)
3. Given a particular Dirichlet boundary condition, solve for the pixel values (height map).
The problem is the resulting height map does not preserve the style of the original height maps, as shown in (C). The reason is because of the arbitrary boundary conditions that we pick. Possible solutions are:
1. Pick some particular boundary condition as attached to the laplacian.
2. Use non-conservative gradient field instead of laplacian image will probably give better result.
Graphcut on image + seam removing on laplacian + poisson init value solving
original terrain (Grand Canyon original size 4096x2048)

The user will give us a rough sketch, we will use some "smart method" to get a rough result using image patches from the original terrain.
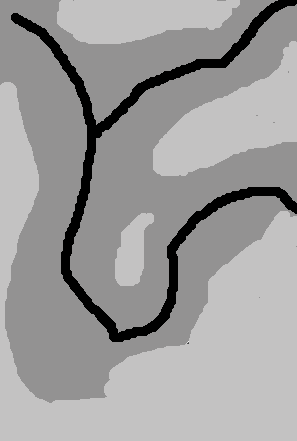 -->
-->

we first removing the seams in the laplacian (known because we put the patches there)
 -->
-->
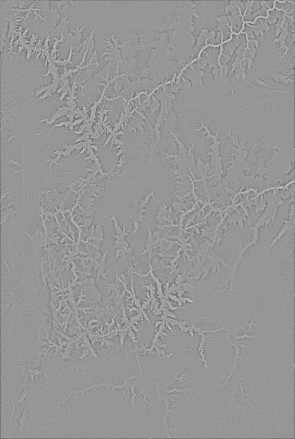
we then smooth the edges of the original image
 -->
-->

We were thinking that now we just need to solve the poisson equation with the modified laplacian and boundary condition, but the result is wrong, because the laplacian field is no longer conservative.

So now, we are thinking instead of solving a boundary value problem, we solve an initial value poisson equation using modified laplacian and boundary. We are currently implementing that idea. (It should work).
Separating high frequency and low frequency + height indexing
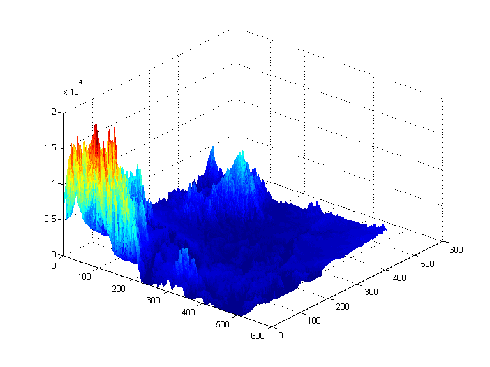
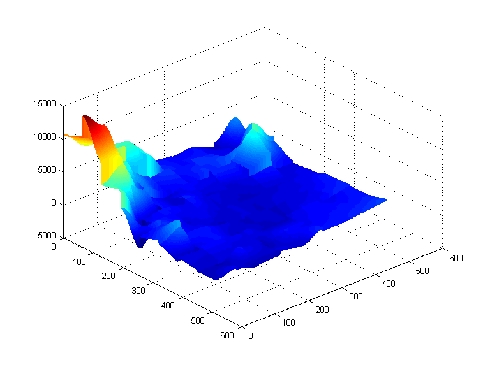

Assumptions:
Algorithm: